Plotting Frequency Spectrum using Matlab

This post shows a variety of ways of how to plot the magnitude frequency content of a discrete signal using matlab.

Contents

• Load Example Data
• Quick view of double-sided (two-sided) magnitude spectrum
• Double-sided magnitude spectrum with frequency axis (in bins)
• Single-sided magnitude spectrum with frequency axis in bins
• Single-sided magnitude spectrum with frequency axis in Hertz
• Single-sided magnitude spectrum with frequency axis normalised
• Single-sided magnitude spectrum – frequency in rads per sample
• Double-sided magnitude spectrum showing negative frequencies
• Single-sided magnitiude spectrum in decibels and Hertz
• Single-sided power spectrum in decibels and Hertz
• Single-sided power spectrum in dB and frequency on a log scale

Load Example Data

% download data from https://www.dropbox.com/s/n4kpd4pp2u3v9nf/tremor_analysis.txt
signal = load('tremor_analysis.txt');
N = length(signal);
fs = 62.5; % 62.5 samples per second
fnyquist = fs/2; %Nyquist frequency

Quick view of double-sided (two-sided) magnitude spectrum

When roughly interpreting this data half way along x-axis corresponds to half the sampling frequency

plot(abs(fft(signal)))
xlabel('Frequency (Bins - almost!)')
ylabel('Magnitude');
title('Double-sided Magnitude spectrum');
axis tight

Double-sided magnitude spectrum with frequency axis (in bins)

fax_bins = [0 : N-1]; %N is the number of samples in the signal
plot(fax_bins, abs(fft(signal)))
xlabel('Frequency (Bins)')
ylabel('Magnitude');
title('Double-sided Magnitude spectrum (bins)');
axis tight

Single-sided magnitude spectrum with frequency axis in bins

X_mags = abs(fft(signal));
fax_bins = [0 : N-1]; %frequency axis in bins
N_2 = ceil(N/2);
plot(fax_bins(1:N_2), X_mags(1:N_2))
xlabel('Frequency (Bins)')
ylabel('Magnitude');
title('Single-sided Magnitude spectrum (bins)');
axis tight

Single-sided magnitude spectrum with frequency axis in Hertz

Each bin frequency is separated by fs/N Hertz.

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_Hz = bin_vals*fs/N;
N_2 = ceil(N/2);
plot(fax_Hz(1:N_2), X_mags(1:N_2))
xlabel('Frequency (Hz)')
ylabel('Magnitude');
title('Single-sided Magnitude spectrum (Hertz)');
axis tight

Single-sided magnitude spectrum with frequency axis normalised

Normalised to Nyquist frequency. Very common to use this method of normalisation in matlab

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_norm = (bin_vals*fs/N)/fnyquist; % same as bin_vals/(N/2)
N_2 = ceil(N/2);
plot(fax_norm(1:N_2), X_mags(1:N_2))
xlabel({'Frequency (Normalised to Nyquist Frequency. ' ...
    '1=Nyquist frequency)'})
ylabel('Magnitude');
title('Single-sided Magnitude spectrum (Normalised to Nyquist)');
axis tight

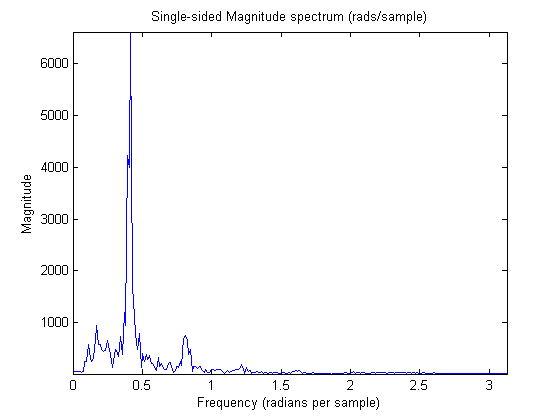
Single-sided magnitude spectrum – frequency in rads per sample

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_rads_sample = (bin_vals/N)*2*pi;
N_2 = ceil(N/2);
plot(fax_rads_sample(1:N_2), X_mags(1:N_2))
xlabel('Frequency (radians per sample)')
ylabel('Magnitude');
title('Single-sided Magnitude spectrum (rads/sample)');
axis tight

Double-sided magnitude spectrum showing negative frequencies

See http://youtu.be/M1bLPZdNCRA for an explanation of negative frequencies

X_mags = abs(fftshift(fft(signal)));
bin_vals = [0 : N-1];
N_2 = ceil(N/2);
fax_Hz = (bin_vals-N_2)*fs/N;
plot(fax_Hz, X_mags)
xlabel('Frequency (Hz)')
ylabel('Magnitude');
title('Double-sided Magnitude spectrum (Hertz)');
axis tight

Single-sided magnitiude spectrum in decibels and Hertz

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_Hz = bin_vals*fs/N;
N_2 = ceil(N/2);
plot(fax_Hz(1:N_2), 10*log10(X_mags(1:N_2)))
xlabel('Frequency (Hz)')
ylabel('Magnitude (dB)');
title('Single-sided Magnitude spectrum (Hertz)');
axis tight

Single-sided power spectrum in decibels and Hertz

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_Hz = bin_vals*fs/N;
N_2 = ceil(N/2);
plot(fax_Hz(1:N_2), 20*log10(X_mags(1:N_2)))
xlabel('Frequency (Hz)')
ylabel('Power (dB)');
title('Single-sided Power spectrum (Hertz)');
axis tight

Single-sided power spectrum in dB and frequency on a log scale

X_mags = abs(fft(signal));
bin_vals = [0 : N-1];
fax_Hz = bin_vals*fs/N;
N_2 = ceil(N/2);
semilogx(fax_Hz(1:N_2), 20*log10(X_mags(1:N_2)))
xlabel('Frequency (Hz)')
ylabel('Power (dB)');
title({'Single-sided Power spectrum' ...
    ' (Frequency in shown on a log scale)'});
axis tight